What is AMD SEV-SNP?
AMD SEV (Secure Encrypted Virtualization) is a technology to isolates guest VMs from the hypervisor.
AMD SEV provides only Memory Encryption.
AMD SEV-ES (SEV Encrypted State) provides encryption for guest VM's registers.
AMD SEV-SNP (SEV Secure Nested Paging) is the latest SEV techonology and it provides strong memory integrity protection and improved attestation.
SEV-SNP has the concept of memory page owner.
Only page owner (guest VM) can read memory page and others cannot read it.
It prevents others from altering memory contents.

(cited from page 7 in AMD SEV-SNP:Strengthening VM Isolation with Integrity Protection and More)
The detail is described in AMD SEV-SNP:Strengthening VM Isolation with Integrity Protection and More
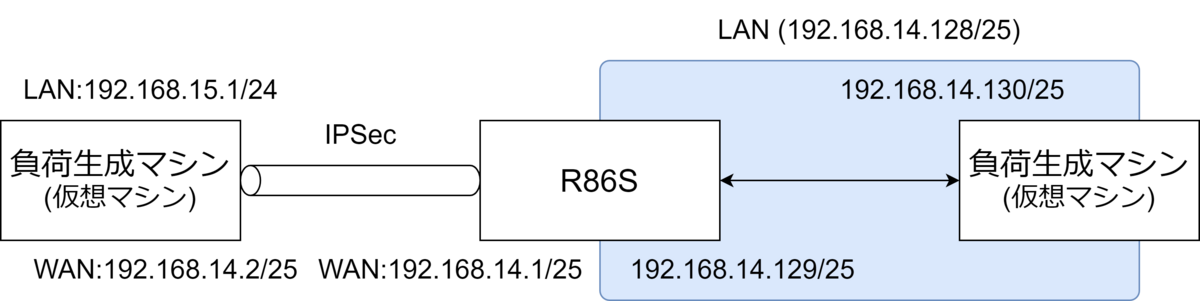
Tested Environment
- CPU: AMD EPYC 7313P
- MotherBoard: Supermicro H12SSL-I (BIOS Version 2.6a)
- Memory: 128GB
- OS: Ubuntu 23.10
Used Software
We need to configure BIOS to enable SEV-SNP support
Advanced -> NB Configuration
- Configure
SEV-SNP Support to Enabled

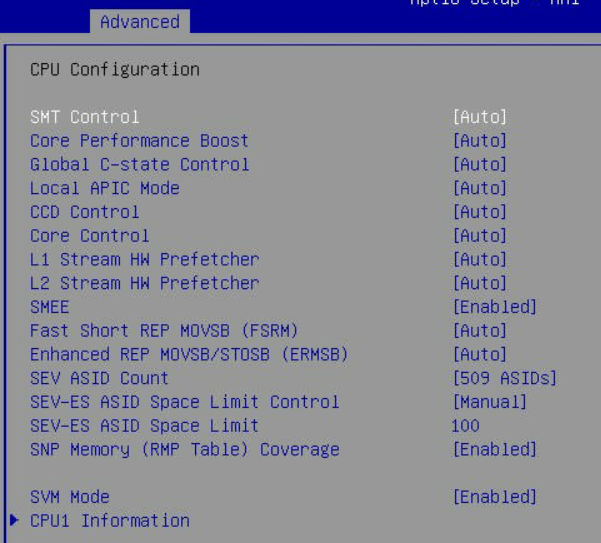
Advanced -> CPU Configuration
- Configure
SMEE to Enabled
- Configure
SEV ASID Count to 509 ASIDs
- Configure
SEV-ES ASID Space Limit Control to Manual
- Configure
SEV-ES ASID Space Limit to 100
- Configure
SNP Memory (RMP Table) Coverage to Enabled
Install the Latest Firmware
Download latest SNP firmware from AMD official Website.
CPU is EPYC 7313P (Millan), so here we download amd_sev_fam19h_model0xh_1.55.16.zip
~$ wget https://download.amd.com/developer/eula/sev/amd_sev_fam19h_model0xh_1.55.16.zip
~$ unzip amd_sev_fam19h_model0xh_1.55.16.zip
Archive: amd_sev_fam19h_model0xh_1.55.16.zip
inflating: amd_sev_fam19h_model0xh_1.55.16.sbin
inflating: Milan Release Notes.txt
~$ sudo rm -rf /lib/firmware/amd/amd_sev_fam19h_model0xh.sbin
~$ sudo cp amd_sev_fam19h_model0xh_1.55.16.sbin /lib/firmware/amd/amd_sev_fam19h_model0xh.sbin
Build Host Kernel for SEV-SNP
Mainline kernel does not have support for SEV-SNP host.
We need to build out-of-tree SEV-SNP supported host kernel.
If you want to build kernel manually, clone source code from https://github.com/AMDESE/linux (branch is snp-host-latest).
Currently(2023/12/30), host kernel commit id is 5a170ce1a08259ac57a9074e1e7a170d6b8c0cda
~$ sudo apt -y install build-essential bison libssl-dev flex libelf-dev libncurses-dev
~$ git clone --single -b snp-latest https://github.com/AMDESE/AMDSEV/
~$ cd AMDSEV
~/AMDSEV$ ./build.sh kernel host
~/AMDSEV$ ls -l linux/
total 342996
drwxrwxr-x 27 naoki naoki 4096 Dec 30 06:42 guest
drwxrwxr-x 28 naoki naoki 4096 Dec 30 06:52 host
-rw-r--r-- 1 naoki naoki 9683256 Dec 30 06:54 linux-headers-6.6.0-rc1-snp-host-5a170ce1a082_6.6.0-rc1-g5a170ce1a082-2_amd64.deb
-rw-r--r-- 1 naoki naoki 88048938 Dec 30 06:54 linux-image-6.6.0-rc1-snp-host-5a170ce1a082_6.6.0-rc1-g5a170ce1a082-2_amd64.deb
-rw-r--r-- 1 naoki naoki 252103406 Dec 30 06:54 linux-image-6.6.0-rc1-snp-host-5a170ce1a082-dbg_6.6.0-rc1-g5a170ce1a082-2_amd64.deb
-rw-r--r-- 1 naoki naoki 1362734 Dec 30 06:54 linux-libc-dev_6.6.0-rc1-g5a170ce1a082-2_amd64.deb
-rw-rw-r-- 1 naoki naoki 7744 Dec 30 06:54 linux-upstream_6.6.0-rc1-g5a170ce1a082-2_amd64.buildinfo
-rw-rw-r-- 1 naoki naoki 2961 Dec 30 06:55 linux-upstream_6.6.0-rc1-g5a170ce1a082-2_amd64.changes
Sucessfully built, deb packages exist. Install them and reboot.
To enable SEV-SNP enabled KVM, module options are required.
debug_swap=0 is required to disable new VMSA fields.
The detail is in https://github.com/AMDESE/AMDSEV/issues/195.
~/AMDSEV$ sudo dpkg -i linux/*.deb
~/AMDSEV$ echo "options kvm_amd sev-snp=1 sev=1 sev-es=1 debug_swap=0" | sudo tee /etc/modprobe.d/kvm.conf
~/AMDSEV$ sudo reboot
Boot from the built kernel.
If everything works correctly, we can see below log.
$ uname -r
6.6.0-rc1-snp-host-5a170ce1a082
$ sudo dmesg | grep -e SEV
[sudo] password for naoki:
[ 0.716831] SEV-SNP: RMP table physical address [0x0000000087800000 - 0x00000000a7dfffff]
[ 5.068960] ccp 0000:47:00.1: SEV firmware update successful
[ 6.904814] ccp 0000:47:00.1: SEV API:1.55 build:16
[ 6.904820] ccp 0000:47:00.1: SEV-SNP API:1.55 build:16
[ 6.916442] kvm_amd: SEV-ES and SEV-SNP supported: 99 ASIDs
[ 6.916444] kvm_amd: SEV enabled (ASIDs 100 - 509)
[ 6.916446] kvm_amd: SEV-ES enabled (ASIDs 1 - 99)
$ ls -l /dev/sev
crw------- 1 root root 10, 122 Dec 30 07:08 /dev/sev
Build SEV-SNP supported QEMU
Build SEV-SNP supported QEMU.
Ubuntu 23.10 has default gcc version 13, but gcc-13 cannot build QEMU correctly.
So, we use gcc version 12 to build QEMU.
~/AMDSEV$ sudo apt install gcc-12 g++-12
~/AMDSEV$ CC=gcc-12 CXX=g++-12 ./build.sh qemu
~/AMDSEV$ ls -l usr/local/bin/qemu-system-x86_64
-rwxr-xr-x 1 naoki naoki 65718848 Dec 30 08:35 usr/local/bin/qemu-system-x86_64
To run linux kernel in SEV-SNP VM, the dedicated UEFI Firmware (OVMF) is required.
To build the dedicated OVMF, we need to patch build script common.sh.
~/AMDSEV$ git diff
diff --git a/common.sh b/common.sh
index e4087d5..171779a 100755
--- a/common.sh
+++ b/common.sh
@@ -126,7 +126,7 @@ build_install_ovmf()
GCCVERS="GCC5"
fi
- BUILD_CMD="nice build -q --cmd-len=64436 -DDEBUG_ON_SERIAL_PORT=TRUE -n $(getconf _NPROCESSORS_ONLN) ${GCCVERS:+-t $GCCVERS} -a X64 -p OvmfPkg/OvmfPkgX64.dsc"
+ BUILD_CMD="nice build -q --cmd-len=64436 -DDEBUG_ON_SERIAL_PORT=TRUE -n $(getconf _NPROCESSORS_ONLN) ${GCCVERS:+-t $GCCVERS} -a X64 -p OvmfPkg/AmdSev/AmdSevX64.dsc"
# initialize git repo, or update existing remote to currently configured one
if [ -d ovmf ]; then
@@ -150,11 +150,11 @@ build_install_ovmf()
run_cmd git submodule update --init --recursive
run_cmd make -C BaseTools
. ./edksetup.sh --reconfig
+ run_cmd touch OvmfPkg/AmdSev/Grub/grub.efi
run_cmd $BUILD_CMD
mkdir -p $DEST
- run_cmd cp -f Build/OvmfX64/DEBUG_$GCCVERS/FV/OVMF_CODE.fd $DEST
- run_cmd cp -f Build/OvmfX64/DEBUG_$GCCVERS/FV/OVMF_VARS.fd $DEST
+ run_cmd cp -f Build/AmdSev/DEBUG_$GCCVERS/FV/OVMF.fd $DEST
COMMIT=$(git log --format="%h" -1 HEAD)
run_cmd echo $COMMIT >../source-commit.ovmf
After modifying common.sh, build the dedicated OVMF.
~$ ./build.sh ovmf
~$ ls -l usr/local/share/qemu/
total 4096
-rw-rw-r-- 1 naoki naoki 4194304 Dec 30 08:25 OVMF.fd
Build Guest Linux Kernel
Build guest linux kernel with SEV_GUEST enabled.
~/AMDSEV$ git diff
diff --git a/common.sh b/common.sh
index e4087d5..b2634d6 100755
--- a/common.sh
+++ b/common.sh
@@ -84,7 +84,7 @@ build_kernel()
run_cmd ./scripts/config --disable SYSTEM_TRUSTED_KEYS
run_cmd ./scripts/config --disable SYSTEM_REVOCATION_KEYS
run_cmd ./scripts/config --disable MODULE_SIG_KEY
- run_cmd ./scripts/config --module SEV_GUEST
+ run_cmd ./scripts/config --enable SEV_GUEST
run_cmd ./scripts/config --disable IOMMU_DEFAULT_PASSTHROUGH
run_cmd ./scripts/config --disable PREEMPT_COUNT
run_cmd ./scripts/config --disable PREEMPTION
~/AMDSEV$ ./build.sh kernel guest
~/AMDSEV$ ls -l linux/guest/arch/x86/boot/bzImage
-rw-rw-r-- 1 naoki naoki 11440128 Dec 30 09:17 linux/guest/arch/x86/boot/bzImage
Run with Measurement
I prepared scripts to launch guest VM with measurement.
Measurement validates memory integrity when the SEV-SNP guest VM starts.
# Setup Rust environment
~$ curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
~$ rustup target add x86_64-unknown-linux-musl
~$ git clone --recursive https://github.com/naoki9911/simple-sev-snp
~$ cd simple-sev-snp
# Build SEV-SNP guest tools
~/simple-sev-snp$ cd snpguest
~/simple-sev-snp/snpguest$ cargo build --target x86_64-unknown-linux-musl
~/simple-sev-snp/snpguest$ cd ../
# Create small initrd with alpine rootfs
~/simple-sev-snp$ ./create_rootfs.sh
# Generate private keys to sign launch digests
~/simple-sev-snp$ ./gen_key.sh
# Then, launch with measurement!
~/simple-sev-snp$ sudo ./launch.sh
# You can get Attestation Report with snpguest
~ # ./snpguest report report.bin req.txt --random
~ # ./snpguest display report report.bin
Attestation Report (1184 bytes):
Version: 2
Guest SVN: 0
Guest Policy (196608):
ABI Major: 0
ABI Minor: 0
SMT Allowed: 1
Migrate MA: 0
Debug Allowed: 0
Single Socket: 0
Family ID:
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
...